four observers of one event

FOUR OBSERVERS SEE EVENT FROM ONE EVENT HORIZON

In December 2006, I found out that my conjecture below, was first accomplished in 1978, and the process is called multilateration. My own realization came in 1994, when I also proposed that a potential use was for air traffic control.

Current theory would have us believe that, not only is the actual event location and event time not determinable but that no such absolute location actually exists...that it all depends upon the observers location.

They conclude that the observation of the event horizon at their personal location is somehow connected to the actual event.

A DISTINCTION MUST BE MADE BETWEEN THE EVENT AND THE EVENT HORIZON.
The event and the event horizon always occur in sequence: the event occurs, ends, then the event horizon occurs and theoretically continues on forever in all directions.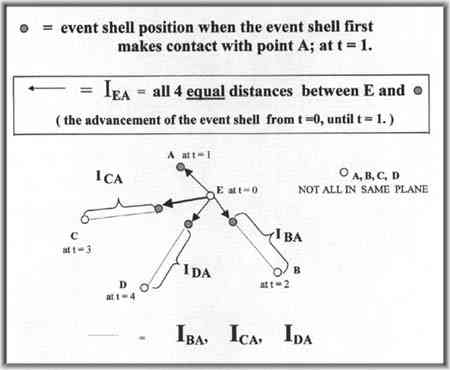

If an event E occurs at t = 0, let point A receive the horizon from event E first at t = 1, B next at t = 2, C at t = 3, D at t = 4.

Let the intervals of receipt times between (A at t = 1) - (E at t = 0) = IEA (B at t = 2) - (A at t = 1) = IBA (C at t = 3) - (A at t = 1) = ICA (D at t = 4 ) - (A at t = 1) = IDA

With a view of a fixed-point space, freeze in place, the location of each observer's fixed-point coordinates at the time of their own individual observation.

Utilizing these time intervals as established above, and these "frozen" four coordinate locations, will mathematically allow an extrapolation to identify the unique single fixed-point location for event E at t = 0. Additionally, the exact universal time of event E will be calibrated by this procedure.

There exists only one length, when added to the interval lengths of IBA, ICA, IDA, that will result in but a single point.

Should any other length is chosen, then it will not be able to solely define a single point.

Choosing a length too short or too long will not allow the interval lengths plus this unique length, the ability to meet at a single fixed-point location.

With this exact length extrapolated later, say at t = 10, combined with this knowledge of the fixed-point locations of these four points and their interval times, then the specific fixed-point location of event E and the specific fixed-interval time of the occurrence at t = 0 can be determined.

THERE EXISTS ONLY 1 FIXED-POINT LOCATION
EXYZ
WHERE
(AXYZ at t = 1 + IEA) =
(BXYZ at t = 2 + IEA + IBA) =
(CXYZ at t = 3 + IEA + ICA) =
(DXYZ at t = 4 + IEA + IDA)

Additionally, there are three more time intervals. Let these intervals between
C - B (t3 - t2) = I CB D - B (t4 - t2) = I DB D - C (t4 - t3) = I DC
ANY of these three intervals could be used mathematically with ANY 3 of the origin 4 intervals, to verify the fixed-point location and fixed-interval time as determined by the original 4 intervals of IEA, IBA, ICA, and IDA.

As an experiment, I would like to physically attempt to replicate the above by use of a challenge in a stadium.