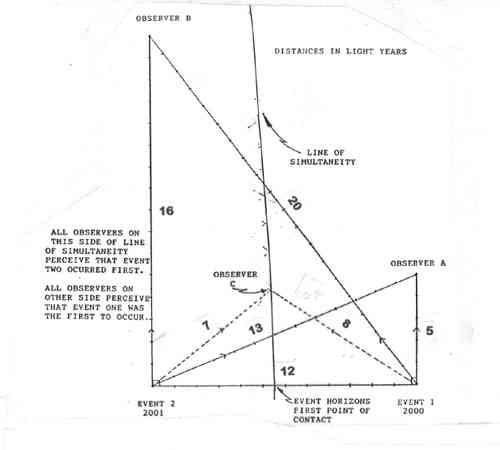
EVENT 1    EVENT 2
 OBSERVER A     2005     2014     SEES light horizon FROM 1 FIRST
 OBSERVER B     2020     2017     SEES light horizon FROM 2 FIRST
 OBSERVER C     2008     2008     SEES light horizon FROM 1 AND 2 AT THE SAME TIME

All points along the line of simultaneity receive the light horizon from event 1 and event 2 at exactly identical moments in time. It is NOT the same instant in time for all places.

The following diagram is a composite of various possible lines of simultaneity. The conditions are that the distance between the two events is 12 years. Let event A happen in the year 2000. Let event B happen in any year from 1989 to 2011.

Although multiple lines of simultaneity are shown in the chart, since event B can really only occur at one time, then in actuality there would be only one such line at a time as was shown in the previous chart.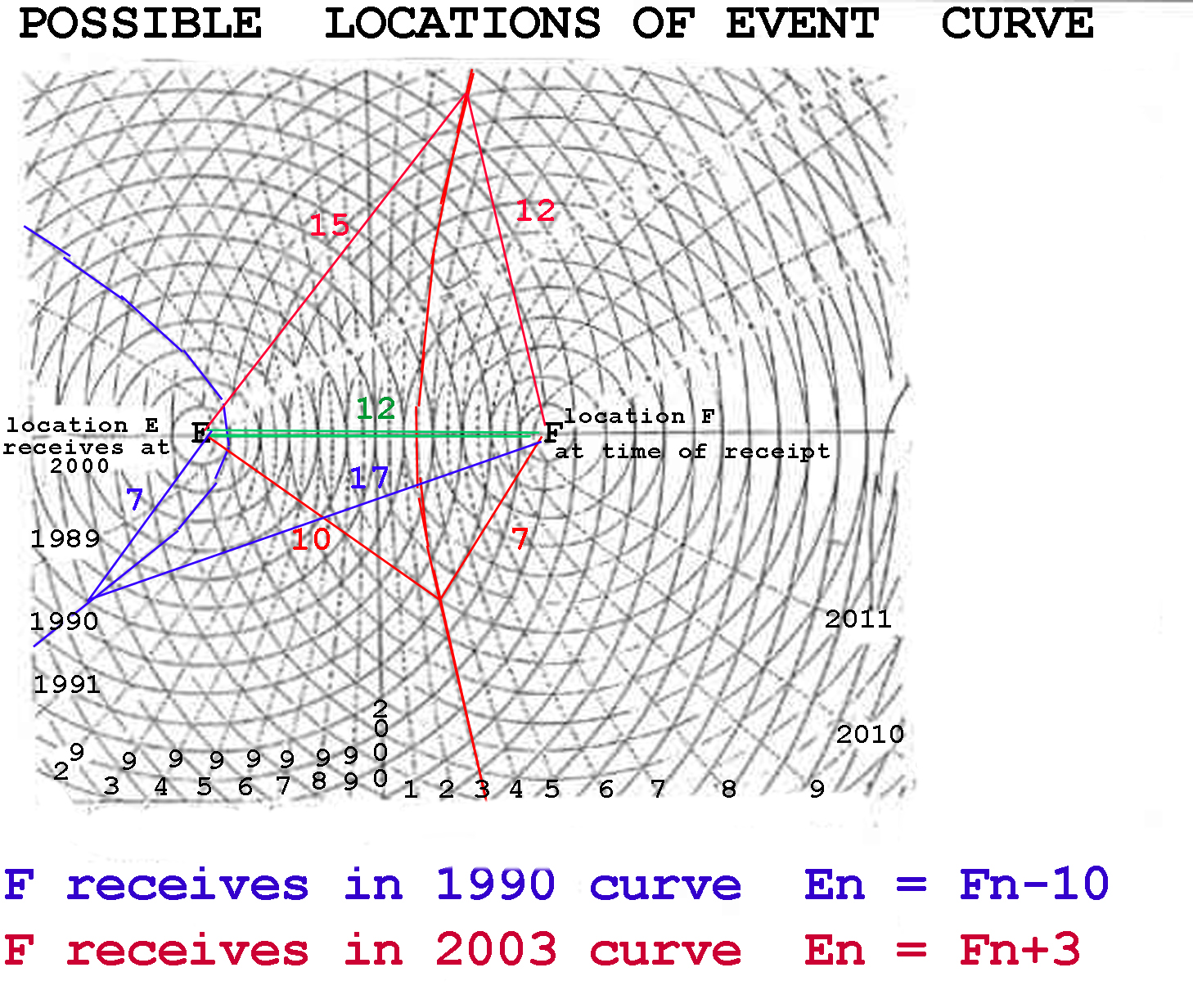





This next chart attempts to isolate the distance (year by year), between the single point of first contact of the event 'horizons' and those locations experiencing simultaneity of those two 'horizons'. Again,as in the previous chart, the elliptical lines only appear due to the composite nature of this chart.



R  =  distance in light years from point of first contact  (between the two event locations)  along the perpendicular and, those points along that perpendicular that are experiencing simultaneity.
T  =  time in light years (commencing from when event 'horizons' first make contact)
D  =  distance in light years between event A and B.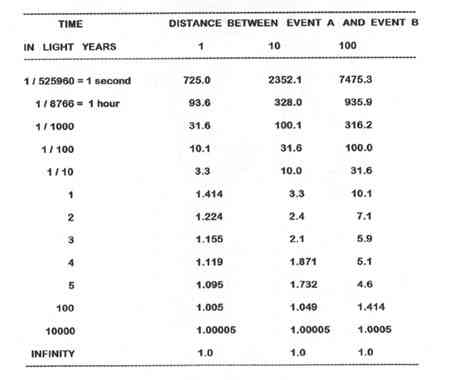



All rates of speed are in units of light years per year, and have been calculated as an average speed from the point of first contact of the two event 'horizons'.

Another way to look at these rates of speed associated with the perpendicular line between the two events and where these event 'horizons' first meet, is to calculate the total distance over some specific time period, such as one year. The following chart shows averages rates of speed during the time period of one year.



These figures are not in contradiction to Newton's laws of motion regarding a body in motion will stay in motion. This is not a body, but an effect. The effect will occur at a decreasing rate and only at infinity does the effect slow to that of the exact speed of light. Nor is this in disagreement with Einstein's second postulate regarding the finite speed of light. This is not light traveling at some speed but simply the effect of two light horizons upon one another over time.

I suggest that not only is this data involving a faster than light effect true, but may indeed have a potential application. This may not just be a mathematical oddity but perhaps the basis of a propulsion system. This propulsion system would be generated by the light waves emitted from two (or more) separate events.

I will supply an example here in the attempt to better visualize these two wave fronts coming together. Imagine yourself in a small boat in a completely calm ocean setting. If we let two explosions occur at the same moment in time and with equal strength producing identical tidal waves and set them off equidistant from your craft, then they should arrive at your position at the exact same moment. By pointing your boat in the right direction, and sailing along the perpendicular, you could let the collision of the two wave fronts push you along.

In a like fashion, the light waves collide and create wave fronts. Since light waves are constantly being emitted, it would be necessary to be able to properly filtered out unwanted waves. Perhaps it would be possible to transmit a signal and have it ride out the wave crest at many times light speed.