june 1999

Arguments against the Galilean coordinate transformation.

Steve Waterman

Abstract
In this paper we will offer some arguments against the Galilean coordinate transformation. We will show that two different coordinates (abscissa) are being assigned to a single point in one reference frame; and in so doing, that a basic mathematical inequality has been generated.
Key words:
coordinate, abscissa, ordinate, origin, Cartesian coordinate system, Galilean coordinate transformation.


1. INTRODUCTION
The Galilean coordinate transformation equations are used to represent the transfer of coordinate positions in one reference frame to their related positions in another reference frame. This requires that the specific change between origins of the two frames is known.
However, what the coordinate transformation actually does, is to transform a line segment value between frames and not the coordinate value. The conclusion that

x' = x - vt. (1)

is valid only when x' is the LINE SEGMENT value.
and not at all correct, however, when x' is a COORDINATE value !

Since the Galilean coordinate transformation equations are indeed intended to be coordinate and not line segment related, the basic question then is, has the coordinate value of x' been properly transformed between frames?
This paper contends, that through the improper use of allowing non-overlapping origins in the same reference frame, this current Galilean transformation procedure causes duplication of coordinates for ALL points in a single reference frame, not just for the conflicting coordinates of point P in question here.
This paper is organized as follows. Section 2 shows the currently accepted Galilean transformation equations and a supporting diagram. Section 3 depicts a challenge to their coordinate transformation procedure. Section 4 supplies proof for that challenge. Section 5 deals with coincidental reference frames. Section 6 deals with non-coincidental reference frames. Section 7 shows the proper coordinate transformation procedure.

2. Currently accepted Galilean coordinate transformation equations and supporting diagram.

Given their following diagram...

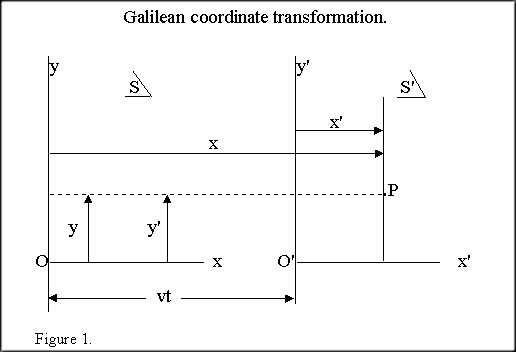The position of point P may be described by the coordinates x and y in frame of reference S, or by x' and y' in S'. S' moves relative to S with constant velocity v along the common x-x' axis. The two origins O and O' coincide at time,
t = t' = 0.(2)

Reference to the figure shows that these are related by
x = x' + vt, y = y', z = z'.(3)

These equations  (2) and  (3) from figure 1, are called the Galilean coordinate transformation equations. (1)



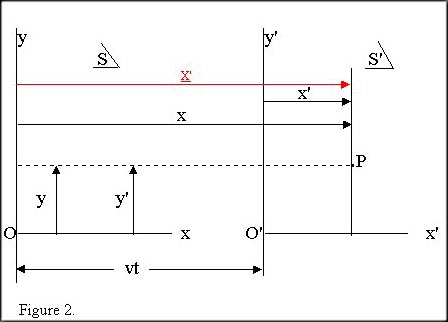
3. After its transformation, has x' now become the total distance from P to the y axis in S as in figure 2 ?
When the Galilean "transforms" x' from one frame to another, it must transfer the coordinate x'. Initially, x' is the abscissa of point P in S', and after "transforming" it, it still is located at point P. Placing x' in this new frame, places the coordinate value x', the abscissa of P, as a second abscissa of P.
After transformation, x' is the coordinate of P in S and therefore also the distance from P to the y axis in S !
(as well as being the coordinate distance from P to the y' axis in S'.)


4. How does x' get to be the abscissa of P in S?
Due to the error of including two origins in one reference frame. If two non-overlapping origins were to be put onto one reference frame, then duplicate coordinates would be assigned to each point.

Logically then, since x' is the given distance from y' to P in S',

A x' is ...the distance from y' to P in S'.
(given)
B x' is ...the abscissa of P in S'.
defined as the horizontal coordinate of a point in a plane Cartesian coordinate system obtained by measuring parallel to the x axis(2).
C x' is ...the first coordinate of P in S'.
Remembering that the definition of a Cartesian coordinate: either of two coordinates that locate a point on a plane and measure its distance from either of two intersecting straight-line axes along a line parallel to the other axis.(2)
D x' is ...the first coordinate of P, is "transformed" to point P in S as x' and now also becomes x' in S. Of these issues listed here (A to G), this should really be the only contentious one. We will attempt to supply additional support for this premise more as a composite of data rather than as a logical sequence.
D1 The Galilean transformation gives the prescription for transforming coordinates of an event from one coordinate system to another.(3)
D2 It is implied (C above), that there is but one origin allowed per reference system. If two origins were allowed, then each point would have additional coordinates and negate the very definition above.
D3 Also not stated in C above but implied, is the fact that each point must have a unique set of coordinates. No point can have more than one set of coordinates. No point may have two different abscissa values in a single reference frame.
D4 With the inclusion of two origins in one frame, as the Galilean does, then an erroneous duplication for the abscissa of P is generated. (and ALL other points as well.)
E x' is now also...the first coordinate of P in S.
Cartesian coordinate: either of two coordinates that locate a point on a plane and measure its distance from either of two intersecting straight-line axes along a line parallel to the other axis.(2)
F x' is ...the abscissa of P in S.
the horizontal coordinate of a point in a plane Cartesian coordinate system obtained by measuring parallel to the x axis(2).
G x' is ...the distance from P to the y axis in S.

Therefore, if the coordinate x' has been transformed, x' is the total distance from point P all the way to the y axis in S and NOT the shorter line segment distance. If the line segment x' is transformed, then no coordinate transformation has occurred.
After proper coordinate transformation then,
x in S =
the abscissa of P in S = (4)
the coordinate x in S = (5)
the line segment (x-vt) in S + the coordinate vt in S = (6)
the coordinate x' in S = (7)
the coordinate x' in S' + the coordinate vt in S = (8)
the coordinate x' in S' + (S-S') = (9)
the abscissa of P in S' + (S-S'). (10)

Specifically then, (for all coordinates and not just the abscissa)...

the abscissa of all points in S =
the abscissa of all corresponding points in S' + the change between origins. (11)

5. Coincidental Cartesian reference frames.
At t is t' is 0,
(x, y, z) = (x', y', z').(12)

With two overlapping origins at time 0, there is NO duplication of coordination.

6. Non-Coincidental Cartesian reference frames.
When t' is > 0, one set of coordinates MUST be different from the other.
ALL points, not just P in this case will differ between frames. That is two different abscissa and ordinate value for each and every point.

7. Proper transformation of coordinates:
All coordinates in one reference frame differ by the same change as has occurred between the two origins. Given this example from figure 3,

Proper coordinate transformation between 2 Cartesian reference frames.


From 2 to 1    (x', y', z')  =  (x + a, y - b, z + a) (13)
From 1 to 2    (x, y, z)  =   (x' - a, y' + b, z' - a) (14)

Conclusions
The Galilean transformation equations incorrectly assign conflicting coordinates to a single point in a single reference frame, not only to this point P in question, but rather to ALL points. Obviously, this would have great impact upon all of the concepts of relativity, including the logic of time dilation and length contraction.

Resume: By virtue of the inclusion of two origins within a single reference frame, the Galilean coordinate transformation incorrectly permits the coordinates of a single point to be assigned two unequal abscissa values. The Galilean fails to properly transform a coordinate value between frames, and has erroneously transformed the line segment value instead, thus creating a basic inequality.
References
1. Sears,Zemansky,Young, University Physics
   (Addison-Wesley 1980)
2. Merriam-Webster, Webster's New Collegiate Dictionary
   (G.& C. Merriam Co.,1973)
3. Kleppner/Kolenkow, An Introduction to mechanics
   (McGraw-Hill,1973)