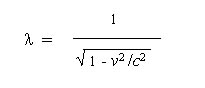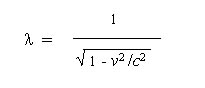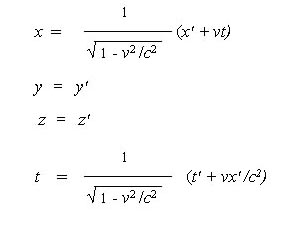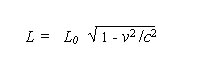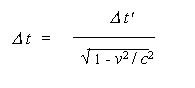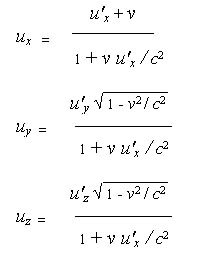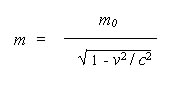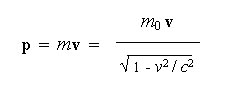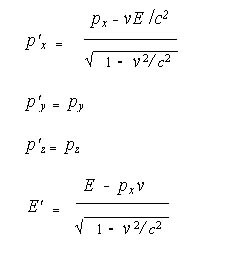june 1999
Arguments against the relativity of length, the relativity of time, the Lorentz transformations equations, the velocity equations, the mass increase formula, and the relativistic momentum formula.
Steve Waterman
|
Abstract |
|
In this paper we will show the trail of formulas predicated from the acceptance of the Galilean transformation equations. This paper will contend that all formulas and equations based solely from these Galilean equations are mathematically invalid as well.
|
|
Key words: |
|
time dilation, relativity of time, length contraction, relativity of length. |
1. INTRODUCTION
The acceptance of
and the disregard of the fact that x' itself now also equals x' + vt (1), is essential to the validity of all of the following well known formulas and equations. Once armed with this initial Galilean inequality, all that is required then, is to make some perfectly acceptable substitutions, then let v equal to c, and simply solve for the various components.
This paper is organized as follows. Section 2 will show the resultant formula that are initially generated by the Lorentz equations through the use of a constant.
Section 3 carries these initial constant
determinations to a breakdown of their components. Section 4 compares their supporting diagram for time dilation (figure 1) with one we have supplied (figure 2) containing some example numerical data.
2. What new equations are generated by the Lorentz equations using the Galilean transformation equations as there basis ?
The specific modifications to (1) by the Lorentz equations may be seen in any university level book on Physics (2).
To summarize their procedure then, they begin the Lorentz transformations by modifying (1), with a constant as yet to be determined. Also undetermined at this point is a form for t, but they will derive it later. Next, the Lorentz substitutes c for v, and then solves for their constant (2).
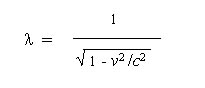 | (2) |
Now they solve for t in terms of t', and in summary, they conclude that
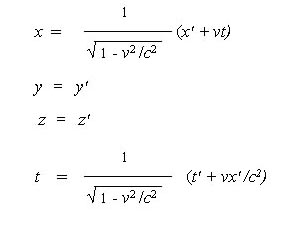 | (3) |
Even at this state of the process, since these are solely based from the inequality of (1), not only is this constant invalid, but so too will be any subsequent formulas derived from this constant formula.
3. What other equations require either the Galilean or Lorentz for their derivation?
From the first of these four equations in (3), they solve for the length and conclude
A the relativity of length, or the length contraction formula.
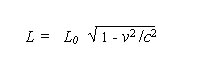 | (4) |
B the relativity of time, or the time dilation formula
From the last of these four equations in (3), they solve for the length and conclude that...
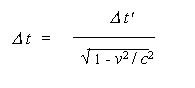 | (5) |
Followed by solving for the velocity,
C the velocity equations,
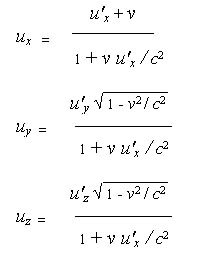 | (6) |
Then solving for the mass component,
D the mass increase formula,
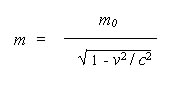 | (7) |
And finally solving for the momentum (8)and its components (9),
E relativistic momentum,
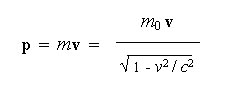 | (8) |
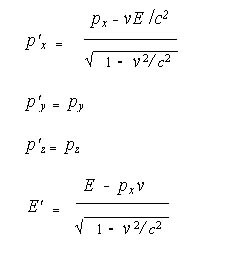 | (9) |
4. What other supporting diagrams are there for any of the above formulas and equations?
Basically only two, one to support time dilation, and the other to support length contraction (not shown here). Each of these initial diagrams represents a situation that does NOT occur. In fact the diagrams appear harmless enough, but hidden in each is another mathematical inequality.
time dilation example
given this accepted example by current Physics...
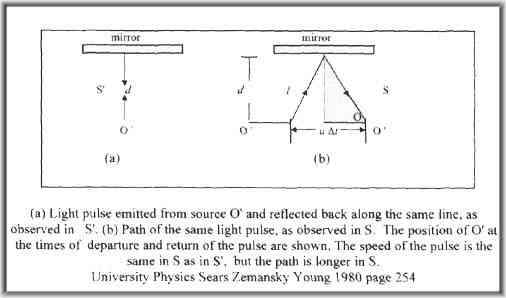
|
My suggested example...
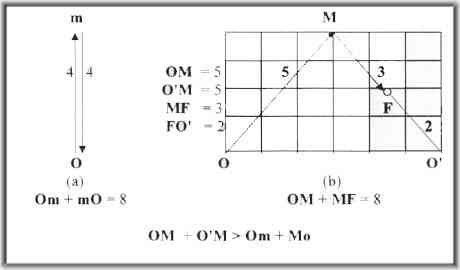
Guaranteed, you can not move to the right, parallel to the mirror, ANY distance from O and be able to detect the return of the light pulse (b) at 8 seconds. (and still also not be point at O.) When the light pulse does return to the parallel of the mirror, the delta t for pulse(a) MUST ALWAYS be less than Delta t for pulse (b).
Since light speed is constant, this initial diagram given by the Lorentz Transformation equation could not actually exist in reality!
CONCLUSIONS
Although the Lorentz transformation substitutions are all mathematically perfectly acceptable, they are derived solely from the Galilean coordinate transformation equations which are invalid. The idea that time or light or mass is in any way is involved, when relating two fixed-point locations to one another, is
invalid. No motion is required in this comparison of locations. The fixed-point
locations differ only in their coordinate value.Light has no inherent impact
upon the transformation of fixed-point locations. The velocity of light, c has no inherent impact upon the transformation of fixed-point locations.
Relativity really sucks. Einstein goofed and we all bought the program. Time ain't screwable. Length don't get squished. Newton has been "absolutely" right all along. It is not just for the observer nor the event, for which absolute time has relevancy. However, it is always the same now, that is being shared simultaneously by all that exists.
When the quantity of observers of a single event exceeds 3, they can determine the specific time and location of that event (in reference to a shared knowledge of their space locations and their shared time demarcations.)
|
Resume: Since the initial premise of the Galilean is wrong, so too are ALL the formulas for the following concepts:
|
|
the relativity of length, the relativity of time, the Lorentz transformations equations, the velocity equations, the mass increase formula, the relativistic momentum formula.
|
References
1. Waterman, see arguments against the Galilean coordinate transformation equations...
2. Sears, Zemansky, Young, University Physics
(Addison-Wesley 1980)
©1999 Steve Waterman